因变量的概率密度¶
导读¶
Hulu机器学习问题与解答系列地三十讲“常见的采样方法”中提到:
很多分布一般不好直接进行采样,此时可以考虑函数变换法。一般地,如果随机变量x和u存在变换关系u=φ(x),则它们的概率密度函数有如下关系:p(u)|φ'(x)|=p(x)。因此,如果从目标分布p(x)中不好采样x,可以构造一个变换u=φ(x),使得从变换后的分布p(u)中采样u比较容易,这样可以通过先对u进行采样然后通过反函数x=φ-1(u)来间接得到x。其中 $p(u)|φ'(x)|=p(x)$ 这个关系并不能一眼看出,下面简单探讨一下。
首先看,对于关系 $y=f(x)$,如果已知 $x$ 的密度函数,如何知道 $y$ 的密度函数?
例子¶
先从一个例子看起:$f(x)=x^2$,即 $y=x^2$。假设 $x$ 有 1000 个取值,在 $[0,1]$ 上均匀分布,$x$ 和 $y$ 赋值如下:
x = seq(0.001, 1, 0.001)
y = x^2
$y$ 的取值范围也是 $[0,1]$。
$x$ 和 $y$ 的形态大致是这样:
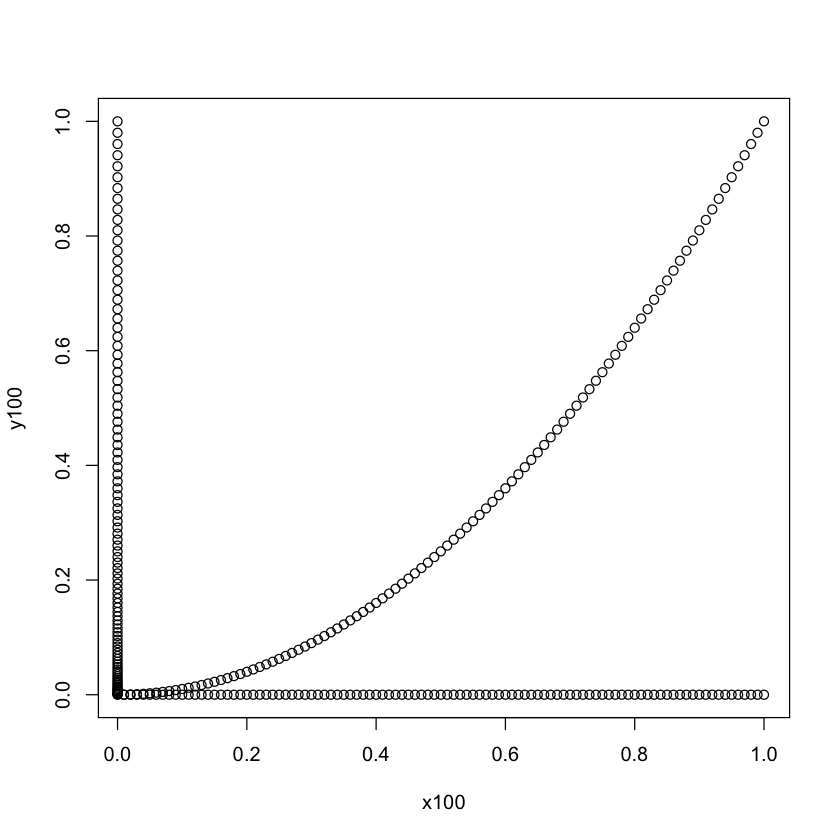
从上图可以看出,$x$ 是均匀分布,$y$ 在靠近 0 的地方更密。
先估算一下 $x$ 和 $y$ 在几个点的密度值。
# 此处计算的是密度,并不是概率密度
density = function (d, window) {
density = c()
points=seq(0.05, 0.95, 0.1)
for (i in points) {
density = append(density, sum(d >= (i - window/2) & d < (i + window/2))/window)
}
return(data.frame(point=points, density=density))
}
density(y, 0.02)
可以看出 $y$ 随着 $x$ 远离 0 点而逐渐稀疏。但是 $y$ 理论密度值是多少呢?
设 $x$ 的密度函数为 $d(x)$。由于在 $[0,1]$ 的范围内 $x$ 有 1000 个点,且均匀分布,则 $d(x)=\frac{1000}{1-0}=1000$。
$y$ 的密度函数需要根据 $y=x^2$ 这个关系和 $d(x)$ 一起求得。(先看效果,证明在后面)
首先找出 $y$ 和 $x$ 的逆运算,即从 $y$ 到 $x$ 的关系:$x=g(y)=y^{\frac{1}{2}}=\sqrt{y}$。
再求得 $g$ 的导数:$g'(y)=\frac{1}{2}y^{-\frac{1}{2}}=\frac{1}{2}\sqrt{\frac{1}{y}}$。
$y$ 的密度函数为 $d(y)=g'(y)d(g(y))=g'(y)d(x)=1000*g'(y)=1000*\frac{1}{2}*\sqrt{\frac{1}{y}}$。
dy = c()
for (y_ in seq(0.05,0.95,0.1)) {
dy = append(dy, 1000 * 0.5 * sqrt(1/y_))
}
data.frame(point=seq(0.05,0.95,0.1), density=dy)
对比上面用离散数据得出的结果,趋势基本吻合。
证明¶
这里要证明的是,已知关系 $y=f(x)$ 和 $x$ 的密度函数 $d_x(x)$,则 $y$ 的密度函数是 $d_y(y)=(f^{-1}(y))'d_x(f^{-1}(y))$。
此处从密度函数 $d(x)$ 转向概率密度 $p(x)$,它们的关系是 $p(x)=\frac{d(x)}{\int_{-\infty}^{\infty}{d(x)}dx}=\frac{d(x)}{Z}$。其中分母 $Z$ 是定积分,是一个常数,不随 $x$ 而变化。
虽然 $d_y(y) \neq d_x(x)$,但是 $Z_y=\int{d_y(y)}dy=\int{d_x(x)}dx=Z_x$,因为 $Z_x$ $Z_y$ 代表的是 $x$ 和 $y$ 的总量。
如果 $p_y(y)=(f^{-1}(y))'p_x(f^{-1}(y))$ 成立,则上面 $d_y(y)=(f^{-1}(y))'d_x(f^{-1}(y))$ 也成立,因为:
\begin{align} p_y(y)=\frac{d_y(y)}{Z_y}=\frac{(f^{-1}(y))'d_x(f^{-1}(y))}{Z_x} \end{align}
下面证明 $p_y(y)=(f^{-1}(y))'p_x(f^{-1}(y))$(参考 spaceisdarkgreen 在 stackexchange 的回答)。
设 $F_x(x) = \int_{-\infty}^{x}p_x(x)dx = P(X \leq x)$ (累积分布函数)。
则,$F_y(y)=P(Y \leq y)=P(f(X) \leq y)=P(X \leq f^{-1}(y))=F_x(f^{-1}(y))$ 。
然而,$F_y(y) = \int_{-\infty}^{y}p_y(y)dy$,所以 $p_y(y)=F_y'(y)$。
最后 $p_y(y) = \frac{d}{d y} F_y(y) = \frac{d}{d y} F_x(f^{-1}(y)) = (f^{-1}(y))'F_x'(f^{-1}(y)) = (f^{-1}(y))'p_x(f^{-1}(y))$ 。
回到导读中提到的关系 $p(u)|φ'(x)|=p(x)$,抛开绝对值符号(为了保证概率非负),可以写成 $p(u)\frac{du}{dx}=p(x)$。
从上面的证明可以得出 $p(u) = (f^{-1}(u))'p(f^{-1}(u)) = \frac{dx}{du}p(x)$ 。
把导数移到左边,得出 $p(u)\frac{du}{dx} = p(u)φ'(x) = p(x)$。完毕。