接受/拒绝采样 (Accept-Reject Sampling)

导读

接受/拒绝采样的目的是利用一个简单（已知）的分布对目标分布（复杂、未知）进行采样。

假设目标分布是 $p(x)$，表示为 $p(x)=\frac{\widetilde{p}(x)}{Z}$，其中 $Z=\int{\widetilde{p}(x)}dx$。

如何从一个已知的分布 $q(x)$ 得到 $p(x)$ 呢？

首先找到一个常数 $M$，使得对于所有的 $x$ 都有 $Mq(x) \geq \widetilde{p}(x)$。

如下图所示。

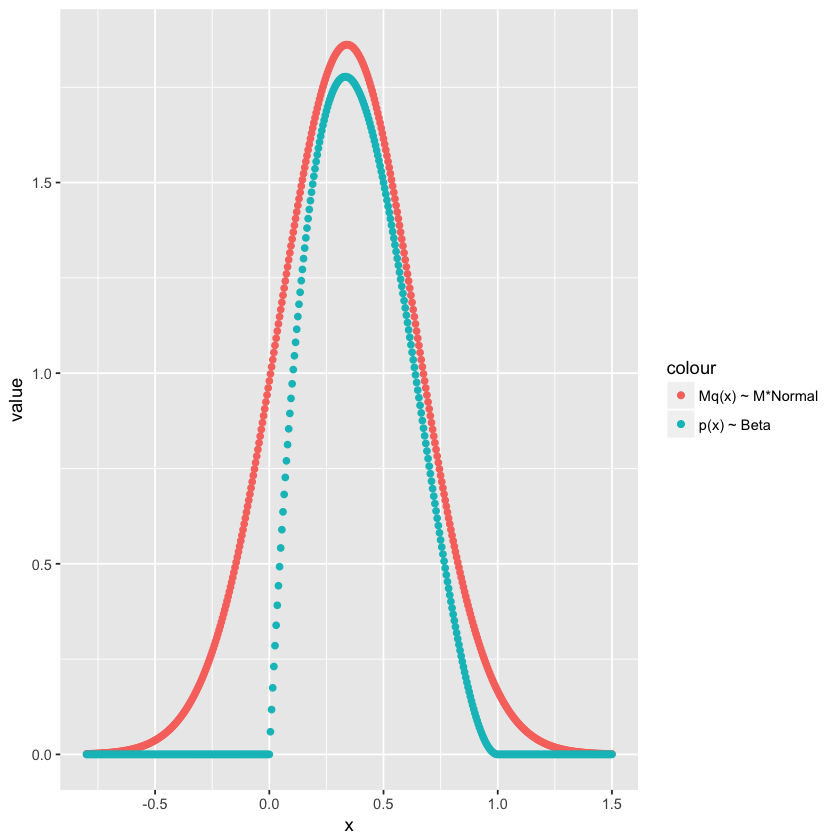
上图中，$\widetilde{p}(x)$ 是 $Beta(2,3)$，$q(x)$ 是 $Normal(0.34, 0.3)$，$M$ 是 1.4。

之后采样的步骤如下：

  1. 从 $q(x)$ 中随机采样得到 $x_i$
  2. 从均匀分布的区间 $[0, Mq(x_i)]$ 采样得到 $u_i$
  3. 如果 $u_i \leq \widetilde{p}(x_i)$ 则保留 $x_i$，否则拒绝 $x_i$，然后重新执行步骤 1 ~ 3，直到获得可保留的 $x_i$

但是重复上面的步骤保留下的 $x_i$ 为什么符合 $p(x)$ 分布呢？

均匀分布

首先来看前两步得到是什么（这两步跟 $p(x)$ 没有关系）。

执行上面的 1 ~ 2 两步，把得到的 1000 个 $(x_i, u_i)$ 标示在图中将得到：

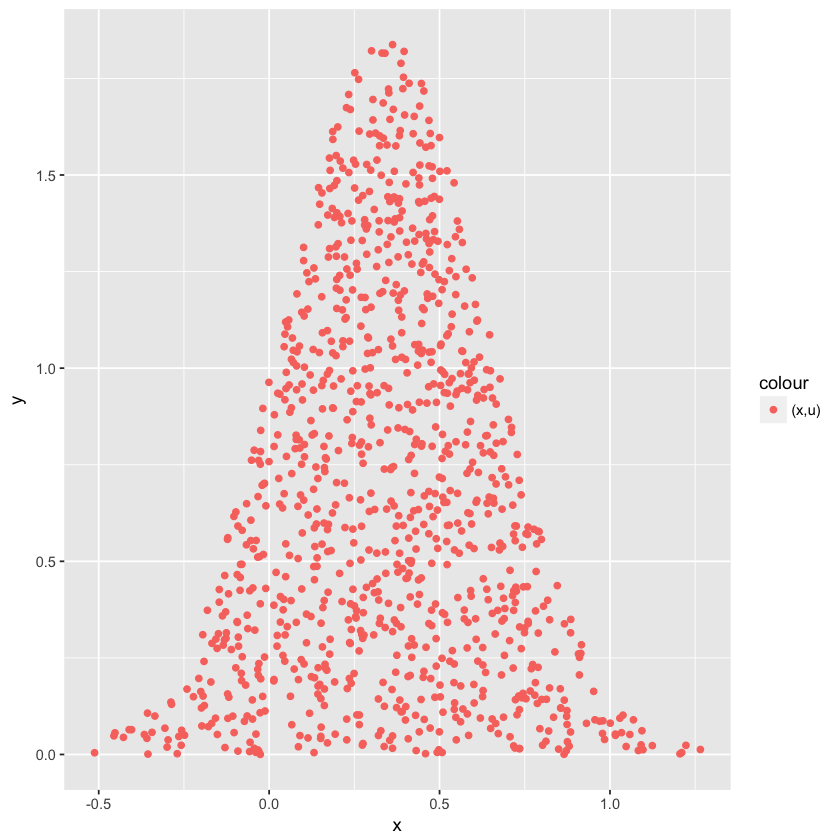
上面图中红点虽然看起来各处有密有稀，但密度理论上是均匀的。

因为选取 $x_i$ 的概率是 $q(x)$，选取 $u_i$ 的概率跟 $Mq(x)$ 成反比，是 $\frac{1}{Mq(x)}$，所以一个点 $(x,u)$ 被选取的概率是 $q(x) \times \frac{1}{Mq(x)} = \frac{1}{M}$，是个常数。即各个区域的概率没有区别。

下面实际估算一下，看看在不同的区域密度大概是多少。

首先为了减少误差，做一个 100,000 的采样：

In [3]:
zs = c()
us = c()
for (i in seq(0,1,length=100000)) {
    zi = rnorm(1, mean=0.34, sd=0.3)
    q  = 1.4 * dnorm(zi, mean=0.34, sd=0.3)
    u  = runif(1, min=0, max=q)
    zs = append(zs, zi)
    us = append(us, u)
}
df100thd=data.frame(x=zs, y=us)

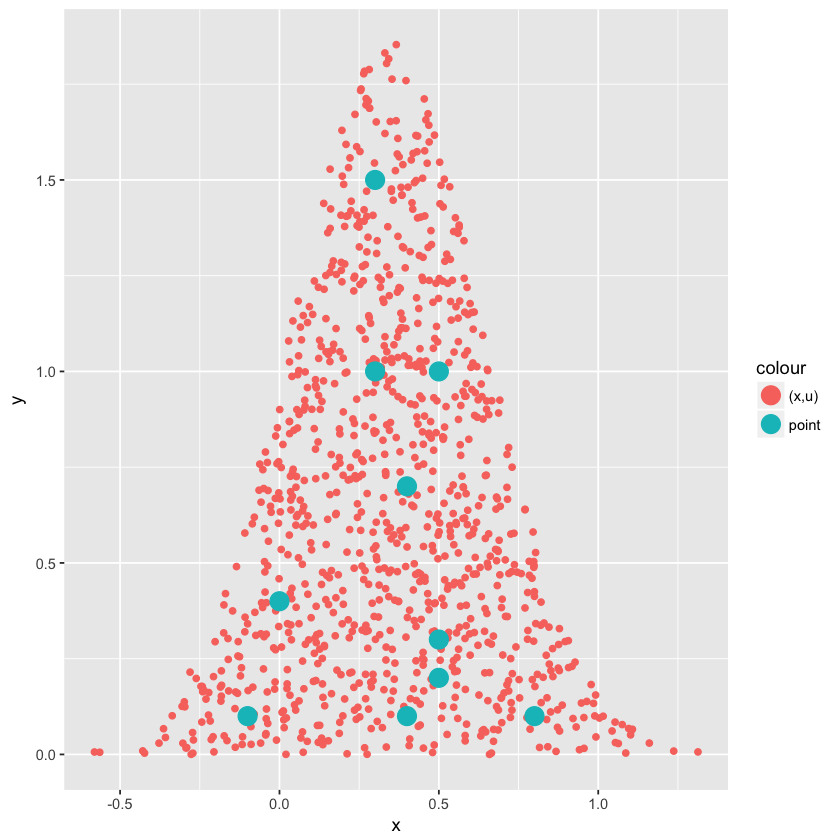
然后看下几个点附近的密度（计算以目标点为中心的正方形内的点数，正方形边长是 0.2）。

几个点在下图绿色圆点的位置：

In [5]:
square = function(p, width) {
    x = p[1]
    y = p[2]
    lowx = x - width/2
    highx = x + width/2
    lowy = y - width/2
    highy = y + width/2
    if (lowy < 0) {
        stop("wrong y")
    }
    if (highy > 1.4*dnorm(lowx, mean=0.34, sd=0.3)) {
        stop("wrong y")
    }
    if (highy > 1.4*dnorm(highx, mean=0.34, sd=0.3)) {
        stop("wrong y")
    }
    return(c(lowx,highx,lowy,highy))
}

in_square_F = function(r,square_) {
    in_square = function(r) {
        if (r['x'] >= square_[1] && r['x'] <= square_[2] && r['y'] >= square_[3] && r['y'] <= square_[4]) {
            return(T)
        }
        return(F)
    }
    return(in_square)
}
In [6]:
points = list(c(-0.1, 0.1),c(0,0.4),c(0.4,0.1),c(0.8,0.1),c(0.5,0.2),
              c(0.5,0.3),c(0.5,1.0),c(0.4,0.7),c(0.3,1.0), c(0.3, 1.5))

for (p in points) {
    print(sum(apply(df100thd, 1, in_square_F(square_=square(p, width=0.2)))))
}

[1] 2896
[1] 2913
[1] 2869
[1] 2862
[1] 2781
[1] 2831
[1] 2917
[1] 2847
[1] 2786
[1] 2974

虽然有些误差，但是可以看出并没有数量级上的差别。

目标分布

再来看第三步。这一步与 $\widetilde{p}(x)$ 比较，扔掉在外面的点，保留在内部的点。

因为 $\widetilde{p}(x)$ 包含在 $Mq(x)$ 内，所以保留下来的点在 $\widetilde{p}(x)$ 内也是均匀分布的。

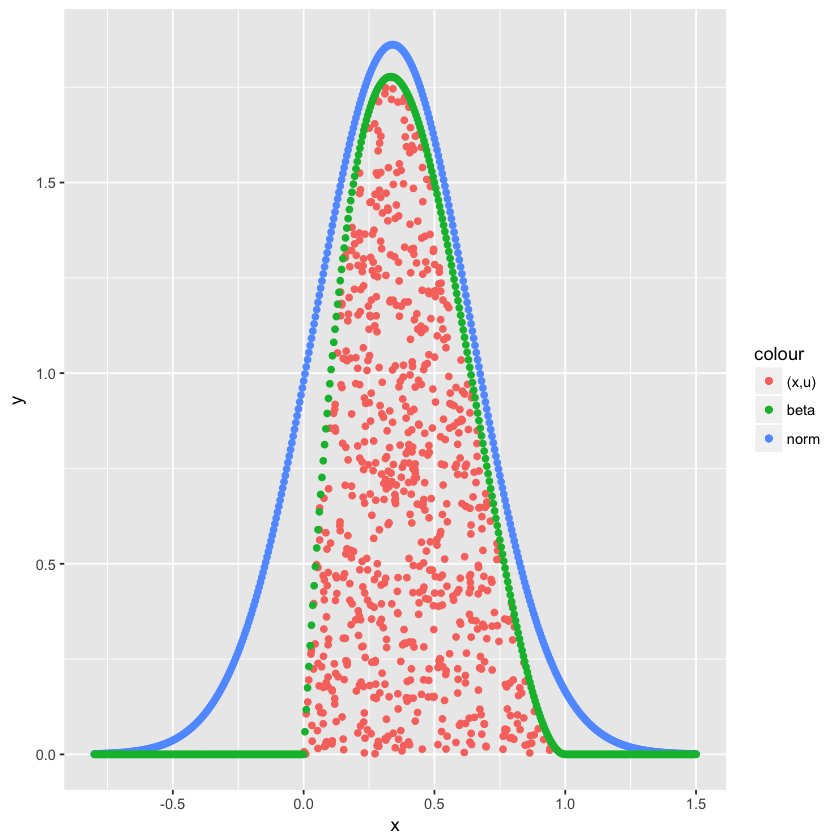
只取这些点的横坐标，即在横坐标上的映射，则这些 $x_i$ 符合 $p(x)$ 分布，因为每个 $x_i$ 的数量跟 $\widetilde{p}(x)$ 成正比。

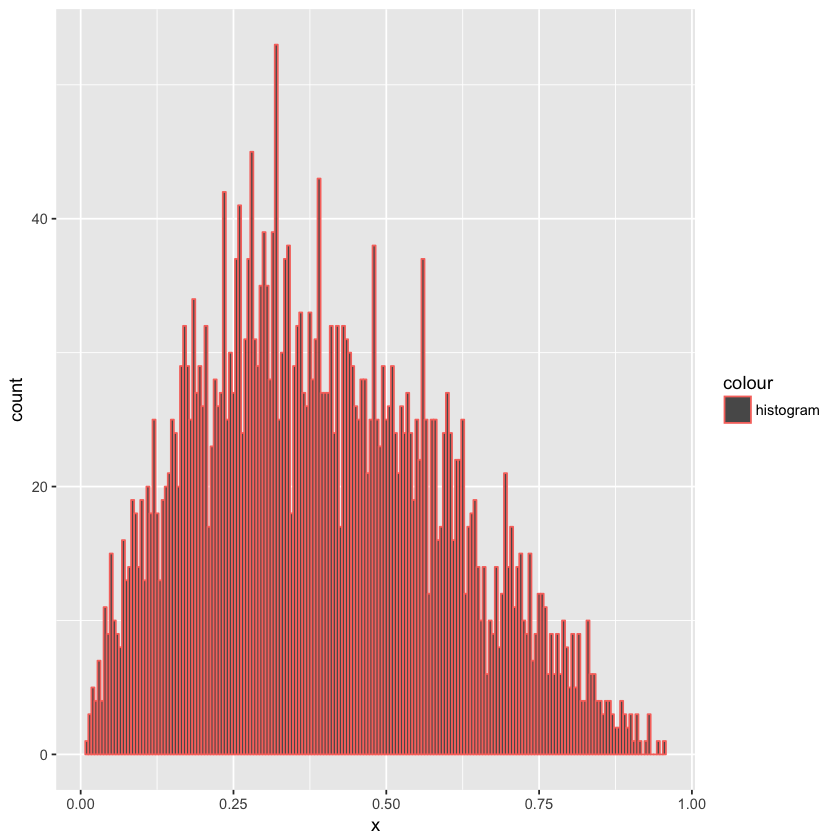
下面是 5000 个采样后 $x$ 的矩形图，大致符合 $Beta(2,3)$ 的形态：

接受率

因为方法中有一定的概率抛弃采样出的点，所以接受率就比较重要了。如果接受率太低，那这个算法的效率就没法接受。

接受率是：$p(accept) = \int{\frac{\widetilde{p}(x)}{Mq(x)}q(x)}dx = \frac{1}{M}\int{\widetilde{p}(x)}dx$ 。其中 $M$ 是一个大于等于 $Z$ 的值，$Z$ 即最开始定义的 $\int{\widetilde{p}(x)}dx$。

理论上 $M = Z$ 的时候，也就是 $q(x) = p(x)$ 的时候 $p(accept) = 1$。

实际上，这个接受率是 $\widetilde{p}(x)$ 下的面积（高维情况下是体积）与 $Mq(x)$ 下的面积之比。由于细微的差别在高维情况下会被指数倍放大，所以变量多的时候，接受率会非常低。导致 Accept-Reject Sampling 只适用于一维和二维的情况，或者在其他采样方法中作为一个子步骤（参考 PRML 11.1.3）。